「N-CG」杂记 01

简介 ¶

简单介绍了一下2D变换的基本概念，以及一些基本的变换矩阵。

文末有一个源于 Computer Vision:
Algorithms and Applications - Richard Szeliski 的表格，总结了2D变换的一些特性。

---

import numpy as np
from matplotlib import pyplot as plt
from Shape import *

0. Base ¶

Note: It’s a 2D base shape. ¶

shape_base = Shape([d(0, 0), d(4, 0), d(3, 2), d(1, 2)], name="Base")
fig, ax = plt.subplots(figsize=FIG_SIZE)
plot_shape_on_ax(ax, shape_base)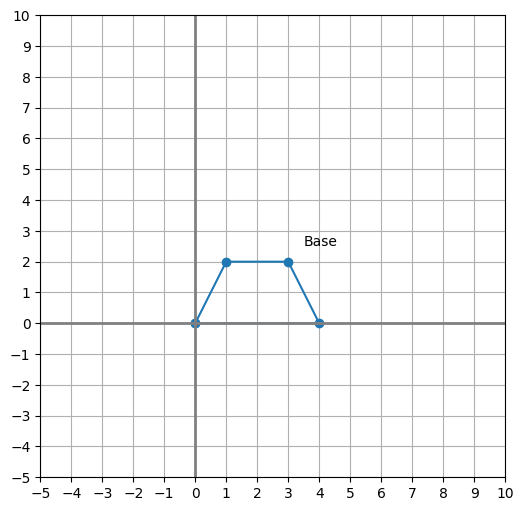

1. Transition ¶

[1, 0, 4],
[0, 1, 2],
[0, 0, 1]

Move the point (x, y) to (x+4, y+2)

Note: For transition, we need to expand the base shape to 3D, and apply a 3D transition matrix. ¶

T_transition = np.array([
    [1, 0, 4],
    [0, 1, 2],
    [0, 0, 1]
])

shape_transition = shape_base.be_dotted(T_transition, name="Transition +4, +2")
plot_shapes([shape_base, shape_transition])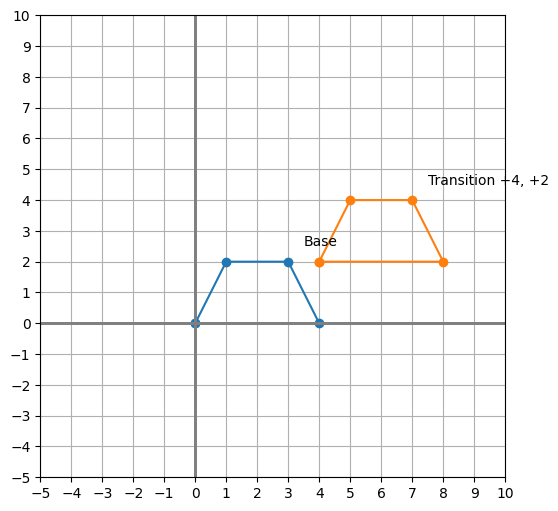

2. Rotation ¶

theta = np.pi/2

    [cos(theta), -sin(theta)],
    [sin(theta), cos(theta)]

Rotate the point (x, y) by 90 degrees counterclockwise

theta = np.pi / 2
T_rigid = np.array([
    [np.cos(theta), -np.sin(theta)],
    [np.sin(theta), np.cos(theta)]
])

shape_rigid = shape_base.be_dotted(T_rigid, name="R -90°")
plot_shapes([shape_base, shape_rigid])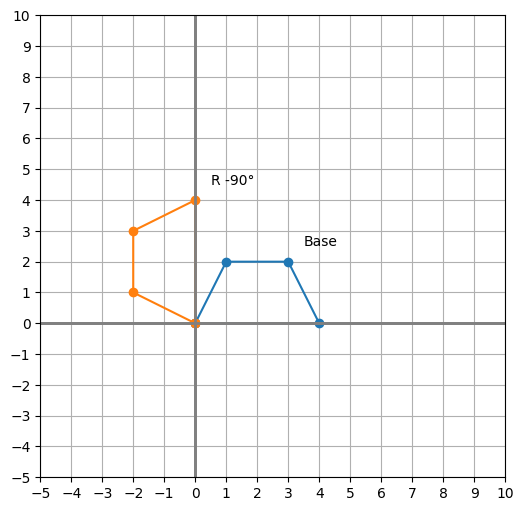

3. Scaling ¶

[2, 0],
[0, 3]

Scale the point (x, y) by 2 in the x direction and by 3 in the y direction.

T_scale = np.array([
    [2, 0],
    [0, 3]
])

shape_scale = shape_base.be_dotted(T_scale, name="Scale 2, 3")
plot_shapes([shape_base, shape_scale])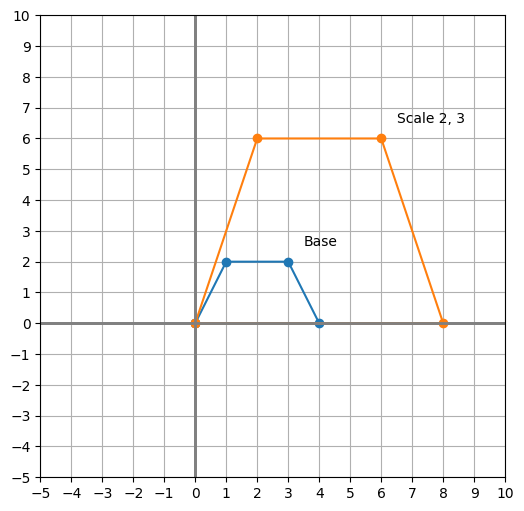

4. Shearing ¶

[1, 2],
[0, 1]

e.g.1: Shear the point (x, y) by 2 in the x direction.

[1, 0],
[2, 1]

e.g.2: Shear the point (x, y) by 2 in the y direction.

[1, 2],
[2, 1]

e.g.3: Shear the point (x, y) by 2 in the x and y direction.

Note: This method is a little bit weried, try understand by calculating the matrix multiplication. ¶

e.g. for T_shear_2, $[[1, 0], [2, 1]] * [4, 0] = [4, 8]$

T_shear_1 = np.array([
    [1, 2],
    [0, 1]
])

T_shear_2 = np.array([
    [1, 0],
    [2, 1]
])

T_shear_3 = np.array([
    [1, 2],
    [2, 1]
])

shape_shear_1 = shape_base.be_dotted(T_shear_1, name="Shear x=2")
shape_shear_2 = shape_base.be_dotted(T_shear_2, name="Shear y=2")
shape_shear_3 = shape_base.be_dotted(T_shear_3, name="Shear x=2, y=2")
plot_shapes([shape_base, shape_shear_1, shape_shear_2, shape_shear_3])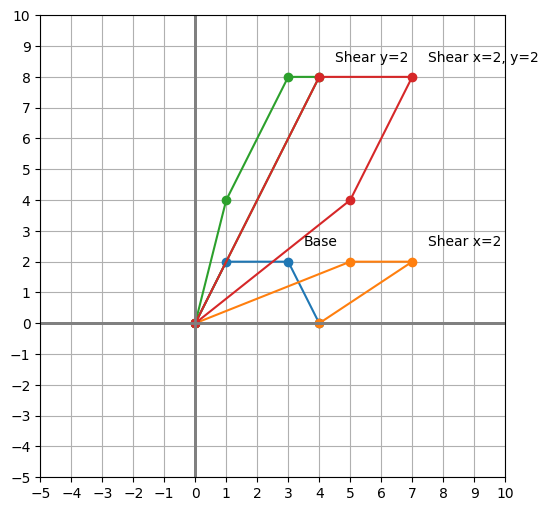

5. Reflection ¶

[1, 0],
[0, -1]

Reflect the point (x, y) over the x-axis.

[-1, 0],
[0, 1]

Reflect the point (x, y) over the y-axis.

[-1, 0],
[0, -1]

T_reflection_1 = np.array([
    [1, 0],
    [0, -1]
])

T_reflection_2 = np.array([
    [-1, 0],
    [0, 1]
])

shape_reflection_1 = shape_base.be_dotted(T_reflection_1, name="Reflect x")
shape_reflection_2 = shape_base.be_dotted(T_reflection_2, name="Reflect y")
plot_shapes([shape_base, shape_reflection_1, shape_reflection_2])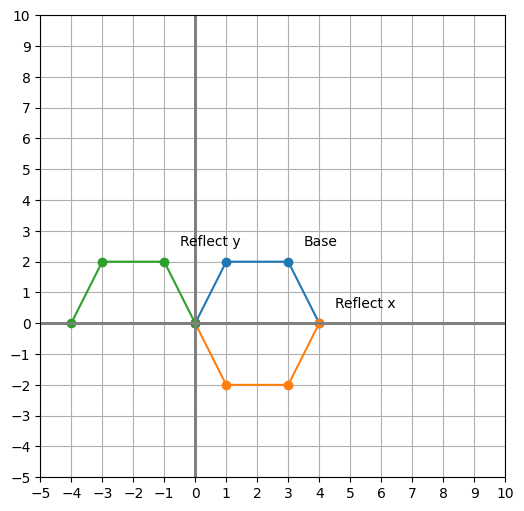

6. Projection ¶

[1, 0],
[0, 0]

Project the point (x, y) onto the x-axis.

[0, 0],
[0, 1]

Project the point (x, y) onto the y-axis.

T_projection_1 = np.array([
    [1, 0],
    [0, 0]
])

T_projection_2 = np.array([
    [0, 0],
    [0, 1]
])

shape_projection_1 = shape_base.be_dotted(T_projection_1, name="Project x")
shape_projection_2 = shape_base.be_dotted(T_projection_2, name="Project y")
plot_shapes([shape_base, shape_projection_1, shape_projection_2])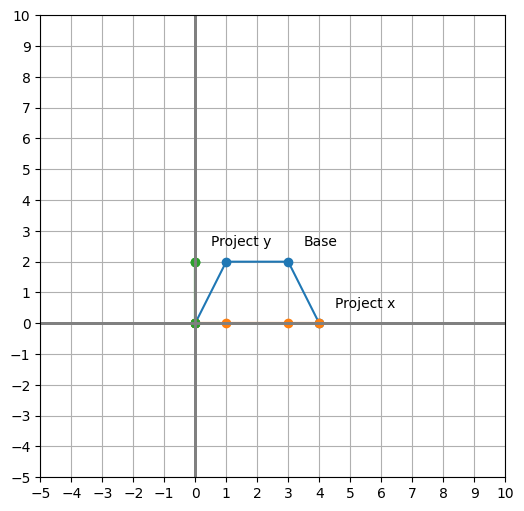

Conclusion ¶

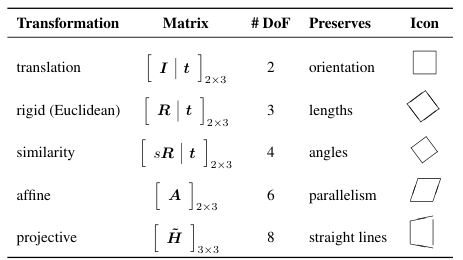
For 2D transformation:

Transformation	DOF	Preserves	Description
Transition	2	Orientation	Move along the x and y axis (2)
Rigid (Eucledian)	3	Lengths	Transition (2) + Rotation (1)
Similarity	4	Angles	Rigid (3) + Scaling (1) Note: Scaling is uniform, which means the scaling factor is the same in both x and y direction.
Affine	6	Parallels	Similarity (4) + Shearing (2)
Projective (Homography)	8	Ratios	Affine (6) + Projection (2)